How gzip uses Huffman coding
I wrote a blog post quite a while ago called gzip + poetry = awesome where I talked about how the gzip compression program uses the LZ77 algorithm to identify repetitions in a piece of text.
In case you don’t know what LZ77 is (I sure didn’t), here’s the video from that post that gives you an example of gzip identifying repetitions in a poem!
I thought this was a great demonstration, but it’s only half the story about how gzip works, and it’s taken me until now to write the rest of it down. So! Without further ado, let’s say we’re compressing this text:
a tapping, as of someone gently
r{apping},{ rapping}
at my chamber door
It’s identified apping and rapping as being repeated, so gzip then encodes
that as, roughly
a tapping, as of someone gently
r{back 30 characters, copy 6},
{back 9 characters, copy 8} at my chamber door
Once it’s gotten rid of the repetitions, the next step is to compress the individual characters. That is – if we have some text like
ab bac ead gae haf iaj kal man oap
there isn’t any repetition to eliminate, but a is the most common letter, so
we should compress it more than the other letters bcdefghijklmnop.
How gzip uses Huffman coding to represent individual characters
gzip compresses bytes, so to make an improvement we’re going to want to be able to represent some bytes using less than a byte (8 bits) of space. Our compressed text might look something like
0101010010101010001010010010010101001010001010100101010101
1001010101010010011111111000000110000100000101000000000000
Those were totally made up 0s and 1s and do not mean anything. But, reading something like this, how can you know where the boundaries between characters are? Does 01 represent a character? 010? 0101? 01010?
This is where a really smart idea called Huffman coding comes in! The idea is that we represent our characters (like a, b, c, d, ….) with codes like
a: 00
b: 010
c: 011
d: 1000
e: 1001
f: 1010
g: 1011
h: 1111
If you look at these carefully, you’ll notice something special! It’s that none
of these codes is a prefix of any other code. So if we write down
010001001011 we can see that it’s 010 00 1001 011 or baec! There wasn’t
any ambiguity, because 0 and 01 and 0100 don’t mean anything.
You might ALSO notice that these are all less than 8 bits! That means we’re
doing COMPRESSION. This Huffman table will let us compress anything that only
has abcdefghs in it.
These Huffman tables are usually represented as trees. Here’s the Huffman tree for the table I wrote down above:
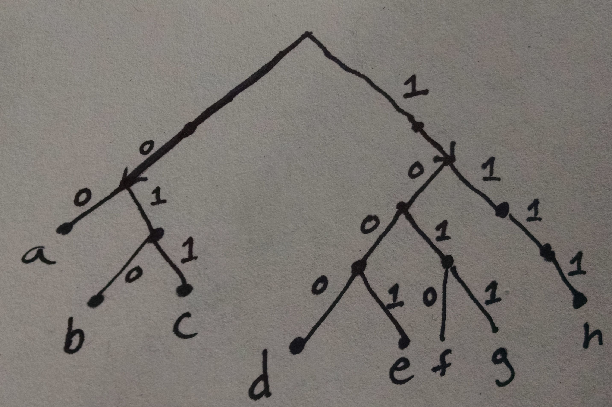
You can see that, for instance, if you follow the path 011 then you get to c.
Let’s read some real Huffman tables!
It’s all very well and good to have a theoretical idea of how this works, but I like looking at Real Stuff.
There’s a really great program called infgen that I found this morning that
helps you see the contents of a gzip file. You can get it with
wget http://zlib.net/infgen.c.gz
gunzip infgen.c.gz
When we run./infgen raven.txt.gz, it prints out some somewhat cryptic output like
litlen 10 6
litlen 32 5
litlen 33 9
litlen 34 10
litlen 39 8
litlen 44 6
litlen 45 9
litlen 46 9
litlen 59 9
litlen 63 10
[... lots more ...]
literal 'Once upon a midnight dreary, while I
match 3 31
literal 'dered weak an
match 5 9
match 3 33
literal 10 'Over many
match 3 62
literal 'quaint
match 5 30
literal 'curious volume of forgotten lore,
This is really neat! It’s telling us how gzip’s chosen to compress The Raven.
We’re going to ignore the parts that make sense (“Once upon a midnight
dreary..”) and just focus on the confusing litlen parts.
These litlen lines are weird! Thankfully I spent 5 straight days thinking
about gzip in October 2013
so I know what they mean. litlen 10 6 means “The ASCII character 10 is
represented with a code of length 6”. Which initially seems totally unhelpful!
Like, who cares if it’s represented with a code of length 6 if I DON’T KNOW
WHAT THAT CODE IS?!!
BUT! Let’s sort these by code length first, and translate the ASCII codes to characters.
' ' 6
'a' 6
'e' 6
'i' 6
'n' 6
'o' 6
'r' 6
's' 6
't' 6
'\n' 7
',' 7
'b' 7
'c' 7
For starters, these are some of the most common letters in the English language, so it TOTALLY MAKES SENSE that these would be encoded most efficiently. Yay!
The gzip specification actually specifies an algorithm for translating these lengths into a Huffman table! We start with 000000, and then add 1 in binary each time. If the code length ever increases, then we shift left. (so 100 -> 1010). Let’s apply that to these code lengths!
' ' 000000
'a' 000001
'e' 000010
'i' 000011
'n' 000100
'o' 000101
'r' 000110
's' 000111
't' 001000
'\n' 0010010
',' 0010011
'b' 0010100
'c' 0010101
'd' 0010110
'f' 0010111
'h' 0011000
'l' 0011001
'm' 0011010
'p' 0011011
'u' 0011100
I found all this out by reading this incredibly detailed page, in case you want to know more.
I wrote a script to do this, and you can try it out yourself! It’s at https://github.com/jvns/gzip-huffman-tree
I tried it out on the compressed source code infgen.c.gz, and you can totally
see it’s source code and not a novel!
' ' 00000
'a' 000010
'e' 000011
'i' 000100
'n' 000101
'o' 000110
'r' 000111
's' 001000
'"' 0010010
'(' 0010011
')' 0010100
',' 0010101
'-' 0010110
I really like going through explorations like this because they give me a better idea of how things like Huffman codes are used in real life! It’s kind of my favorite when things I learned about in math class show up in the programs I use every day. And now I feel like I have a better idea of when it would be appropriate to use a technique like this.