Day 13: BPTT, and debugging why a model isn't training is hard
Hello! I spent the last couple of days experimenting with using back propagation through time with RNNs.
debugging “this isn’t training” is hard
Yesterday I was training a model,and the loss over time looked like this:
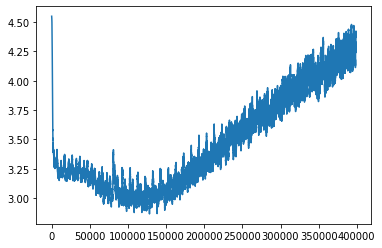
Basically, it went down for a while, and then it went back up a LOT. I still have no idea why this happened: if the optimizer was struggling to optimize, I’d expect the loss to get stuck and plateau and maybe wobble around, but not just keep going up forever. This makes no sense to me yet.
I drew a corresponding graph of the norm of the gradient of one of the weight matrices to go with this, because I kept reading about “vanishing gradients” and “exploding gradients” and I wanted to see if I was suffering from them. Here’s the graph:
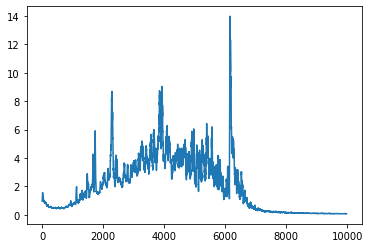
I think this graph might be showing me a vanishing gradient – the norm of the gradient does get pretty small towards the end of the graph.
BPTT: back-propagation through time
I’ve been experimenting with a different way of training my RNN: instead of writing code like this, which trains one character at a time.
for input, target in training_data:
output, hidden = model(input, hidden)
loss = F.cross_entropy(output, target)
optimizer.zero_grad()
loss.backward() # calculate the derivative
optimizer.step() # adjust weights
hidden.detach()
instead I’m giving it a bunch of data (ok, the sentence is ‘a’, ‘b’, ‘c’, ’d’, ’e’, ‘f’… ) and then only doing the gradient descent/backpropagation step periodically. The code looks a little like this:
for i, (input, target) in enumerate(training_data):
output, hidden = model(input, hidden)
# only do the optimizer step 10% of of the time
if random.randint(0, 10) == 2:
loss = F.cross_entropy(output, target)
optimizer.zero_grad()
loss.backward() # calculate the derivative
optimizer.step() # adjust weights
hidden.detach()
Some questions I have about this:
- When I do BPTT after every 40 steps, the model fails to train (it has the “improve and then get worse” behaviour I graphed above), but when I do it after 10 steps it works fine. Why?
- When I trained on (I think??) the same training data with the one-character-at-a-time method, the model learned a lot of character names (like CYMBELINE). When training it with BPTT it seems not to have learned any character names. I’m not yet sure if this is a difference in the training data or if I need to do something different with the model.
waiting for training to finish is frustrating
I’ve spent way too much time over the last couple of days waiting 30 minutes for a model to train so I can tell if it’s working or not. I’m not sure how to handle this yet, but I need either a faster feedback loop or something to do while I’m waiting.
I think the main reason this is frustrating is that I have a lot of hypotheses I want to experiment with, but it takes so long for every one and it’s a bit hard with a Jupyter notebook to keep track of all the hypotheses I’m trying to track.
should I be doing gradient clipping?
Recently I added “gradient clipping” to my training function. Basically I think this means that if the norm of the gradient is bigger than some value (like 1), then the optimizer scales the gradient so that it has a smaller norm.
It’s only one line of code, but I can’t tell if it’s helping yet
torch.nn.utils.clip_grad_norm_(self.rnn.parameters(), 1)
open questions
I’m just going to recap some of my open questions for myself in case I can answer them in the next post.
- is doing gradient clipping helping?
- why does the loss for my model climb so much? why is that even possible?
- why does BPTT with a sequence length of 40 not work, but a sequence length of 10 work?
- does randomizing the sequence length with BPTT help?
- is it an “exploding gradient” if the norm of the gradient goes up to 12? (i think the answer might be “no”?)
- is it a “vanishing gradient” if the norm of the gradient goes down to 0.05? (i think the answer might be “yes”?)
- does the
seq_lendimension in PyTorch’s LSTM class refer to BPTT? (in other words, do I have to implement BPTT myself or will that LSTM class do it for me if I format my data the right way?) - how can I tell if I’m having numerical stability issues?
Maybe I can answer some of those questions next!
some text the BPTT model generated
that than their conirot-ula thine not wate) For then in that my shill, And
Time, Wiss envage so love at thes: Time worture women of their cay bu thee
wisted all Tom werthen hear momed. An is perselfed? Bu mundeve teassed for my
sead wherey tood the ob'e, With eres, The ecref of heaven. 25 Levery I t
This seems really similar to the non-BPTT text:
at soerin, I kanth as jow gill fimes, To metes think our wink we in fatching
and, Drose, How the wit? our arpear War, our in wioken alous, To thigh dies wit
stain! navinge a sput pie, thick done a my wiscian. Hark's king, and Evit night
and find. Woman steed and oppet, I diplifire, and evole witk ud