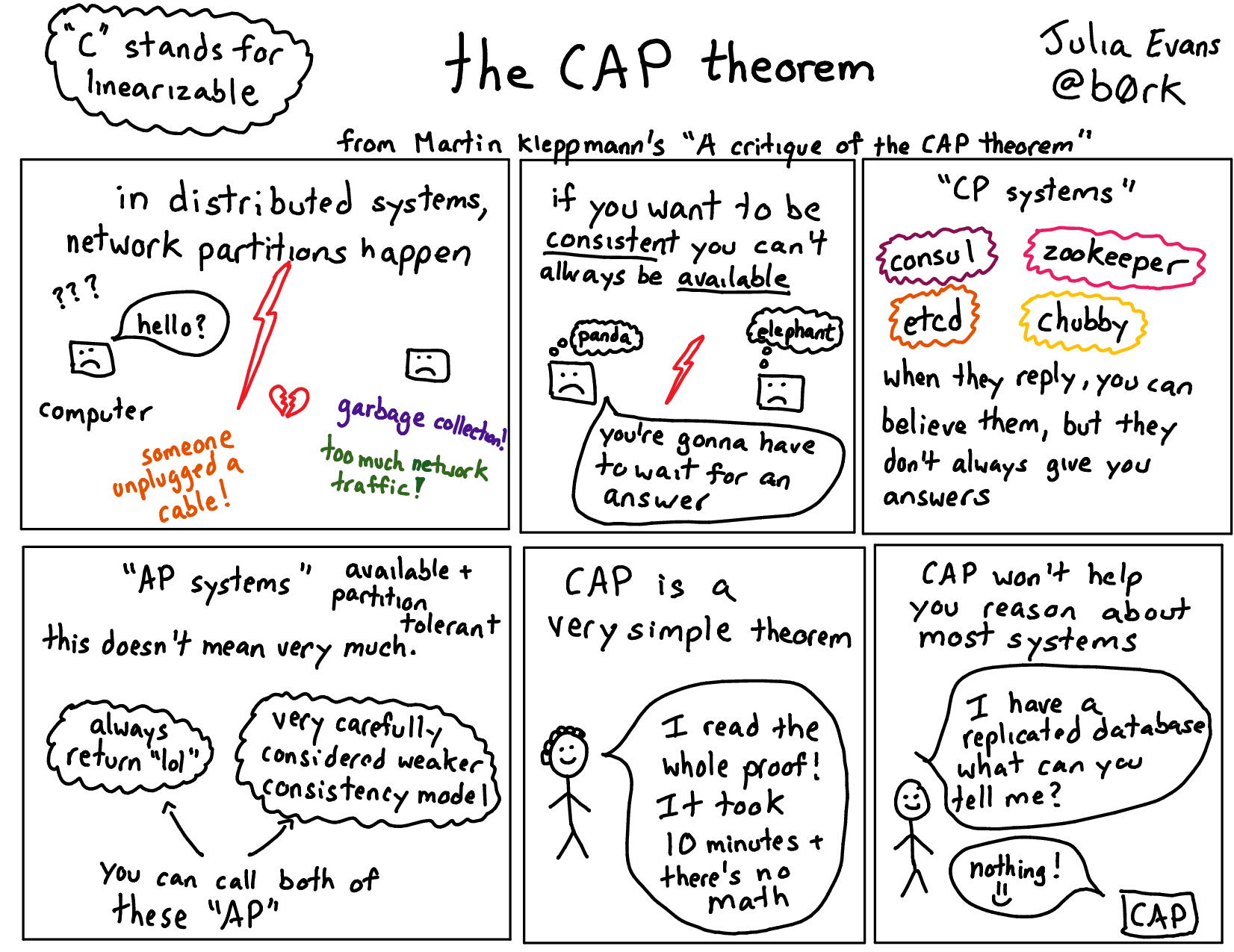
"A Critique of the CAP Theorem"
This week I read a paper called A Critique of the CAP Theorem by Martin Kleppmann. I thought it was super interesting and I wanted to tell you why! And maybe convince you to read it.
The CAP theorem is an often-cited result in distributed systems research. It basically says that, if you have a real-world database that runs on more than one computer, it can either offer
- linearizability (which I won’t explain here, but is a specific consistency requirement. There’s a pretty good explanation in this blog post)
- or availability (every computer in the system can always give you a response)
This theorem is sometimes phrased as “consistency, availability, or partition tolerance, pick 2”, but we’ve established pretty well at this point that you can’t sacrifice partition tolerance, so you just get to pick between C and A. If you want more examples of network partitions, there’s this very long list by Kyle Kingsbury of examples of network partitions happening and having serious consequences.
As usual i’m not a distributed systems expert and probably something in this post is wrong.
is the CAP theorem actually useful?
Some distributed systems claim to be linearizable, like Consul and etcd and zookeeper. These use algorithms like Paxos or Raft. The CAP theorem is a little bit useful for reasoning about these systems – because they’re linearizable, they must not be totally available. You should expect some downtime from those systems in practice. Good! That was useful. Thanks, CAP theorem!
I have some extremely small amount of experience working with linearizable systems, and in my experience those systems are actually not always available! So this theorem also actually really does match up with what happens in real life, which is cool.
Okay, but what about every other distributed system? For example! What if I’m using a database system that has a primary and replicates writes to a secondary, and then I read from the secondary sometimes?
This system is not linearizable. So the CAP theorem has… uh… nothing to say about this system. But replicated database setups are extremely common and extremely useful! It seems silly to just stop at “well, that’s not linearizable, I have nothing else to say”. “AP” is not a very useful description for this system since it has some interesting consistency properties, and is quite different from some other “AP” systems.
the proof of the CAP theorem is extremely simple
I thought that the CAP theorem was like this complicated deep result in distributed systems theory.
It turns out that (even though it is a somewhat useful thing!) it is a really simple result to prove. Basically:
- you have 2 computers
- suppose those two computers can’t communicate
- suppose furthermore that you want them to act consistently (if you write “hello” to Computer 1, you want the whole system to know the value is “hello”)
Now suppose you ALSO want the system to be available. This is impossible! Computer 2 can’t tell you that the current value is “hello”! There is no possible way it could know that because it can’t communicate with Computer 1!
That’s basically the whole proof. You need to formalize it a bit by defining things clearly which is why the paper is several pages instead of 2 paragraphs. (definitions are important)! But the core idea is just not complicated. For more, see this illustrated guide and the original paper, but the proof is not fundamentally more complicated than that.
To me this undermines the theorem a little bit – CAP is a useful shorthand for a useful idea, but it’s not realy that profound. By contrast, the FLP impossibility theorem shows that is it impossible to build a distributed consensus algorithm that will always terminate. (so there’s some risk that an algorithm like Paxos/Raft will get stuck in an infinite loop). This seems a lot less obvious (and was an open question for a long time).
is there a general tradeoff between consistency and availability?
So, once we’ve learned about the CAP theorem, we might hope that in addition to the specific rule (if you’re linearizable, you can’t be available), there might also be some more general tradeoff (if you’re a little bit more consistent, then you get a little bit less available).
This feels like a totally reasonable thing to hope. The CAP theorem does not actually say anything about this hope, but maybe it’s true anyway!
What happens when your network gets slow?
My favorite thing about this critique of the CAP theorem is it PROPOSES A USEFUL ALTERNATIVE THEOREM. (the “How operation latency depends on network delay” section of the paper)
Let’s suppose your network gets SLOW. (Kleppmann defines this a little more formally but I’m gonna go with SLOW)
Well!! If you’re using a linearizable system, it means that your reads are slow, and your writes are slow. That sucks!
What if you trade off and have a system which is a little less consistent? It turns out that if you want “sequential consistency”, you can have slow writes, but fast reads! That sounds a little like our replicated database situation, maybe! (you could imagine that writing to the primary could get slow).
Here is a table from the paper where he tabulates different consistency levels and how fast of reads/writes you can get under adverse network conditions.
| consistency level | write | read |
|---|---|---|
| linearizable | slow | slow |
| sequential consistency | slow | fast |
| causal consistency | fast | fast |
In particular this means that if your network is totally down, then writes in a linearizable system take an infinite amount of time (so writing is actually impossible).
why this is awesome
I think this different framing (where we talk about availability in terms of network latency & speed of operations) is really cool, because:
- it actually relates better to my real life (sometimes my network is not totally down, but communication is SLOW! I would love my distributed systems theory to explain what will happen!)
- it lets me describe more systems! I feel almost motivated to learn what “sequential consistency” and “causal consistency” even mean now to see if any of the systems I actually use match that definition.
The last kind of silly reason I think this is awesome is – I spent a really long time feeling bad that I didn’t understand the CAP theorem or know how to apply it. It turns out that the CAP theorem is actually a relatively small theorem which is only useful in a limited number of cases! So it was less that I didn’t understand it and more that it’s actually just not thaaaaaaat useful. Now I don’t feel as bad! And I have some slightly better tools for thinking about distributed systems! Yay.
On my reading/watching list:
- availability & consistency by Werner Vogels
- more about the FLP theorem
- CAP 12 years later