And it’s actually useful?!

Paul Wankadia sent me an email yesterday about regular expressions and I thought it was so interesting I decided to write up some of what I learned from it. I thought I knew how regular expressions worked on computers because I took a class on them in university (hi prakash), but it turns out that no, I did not know.

The email was about a couple of regular expression libraries he works on: RE2, Google’s regular expression library, and redgrep.

I did not know what RE2 was, and it is the older library, so let’s start there.

regular expressions: the university class

I took a class on regular expressions in university. In them, I learned that you have “regular languages”, which can be matched by deterministic finite automata, or DFAs. I’m not going to explain what those are here because I do not have space but here is a DFA. It has two states, and its job is to detect strings with an even number of zeroes.

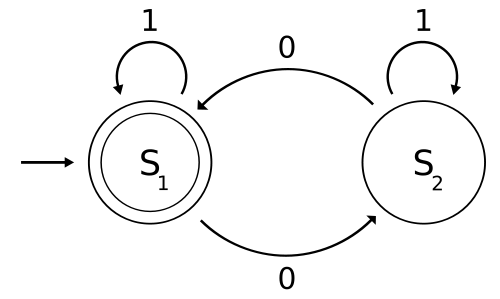
So, if you’re trying to see if the string “00100” matches, you’ll go

* start: S1
* see a 0: go to S2
* see a 0: go to S1
* see a 1: stay on S1
* see a 0: go to S2
* see a 0: go to S1
* S1 is an "accept" state because of the two circles around it!
that means that the string 0000 matches! Yay!

In any class like this, you’ll prove that any regular expression can be represented as an NFA (nondeterministic finite automaton), which can in turn be translated into a DFA (like the picture above). if you never took this class this may be confusing and I apologize.

the important thing to know is: DFAs are simple and fast and very nice. they are state machines!

how do you do regular expressions on a computer?

So, now suppose that we have the regular expression (1*01*0)* to match any string with an even number of zeroes. That is the same as the DFA (above) and you might expect that it is actually implemented by… coding up a DFA as a state machine. Right? We said that DFAs are simple and beautiful and amazing and so the regular expression implementers probably used them.

Apparently this is not true! Our next stop is a series of posts on regular expressions by Russ Cox, who originally wrote the RE2 library (release blog post). I think the best place to start is Regular Expression Matching Can Be Simple And Fast (but is slow in Java, Perl, PHP, Python, Ruby, …). This is a very good clickbait title, and lives up to its promise by also being an excellent article.

I’m not going to try to explain the article (you should just read it! it is very clear.), but it basically says

• ken thompson wrote a great regular expression search algorithm in the 60s
• perl & friends use a different algorithm (backtracking) that has worse worst-case complexity (exponential)
• at google they care about worst-case complexity because they would like their regular expressions to never explode exponentially in complexity.

The ken thompson paper where he introduced this is called Regular expression search algorithm. I think this is more like using a DFA than like backtracking, but it does not create the DFA explicitly (because there can be an exponential blowup there for the same reasons, and you so you don’t want to do it upfront).

RE2 uses an approach more like this ken thompson approach, so that no regular expression can explode and take forever.

Awesome. Let’s move on.

regular expression derivatives and redgrep

everything up to here made sense to me. Apparently, though, there’s more! in the next step of being a regular expressions nerd, we talk about “regular expression derivatives”. This idea comes from a paper “Derivatives of Regular Expressions” by Janusz Brzozowski. (link where you have to pay to download the paper, but, sci-hub.io exists). Here is the wikipedia article.

But we can describe some of the ideas in words. Let’s say we have a regular expression which is supposed to match the strings (‘a’, ‘abab’, ‘aaaabb’, ‘bbc’).

The derivative of those strings with respect to 'a' is (’’, ‘bab’, ‘aaabb’) – you strip off the a from every string.

It turns out (which is not totally obvious to me, but I think if you go through all the cases it’s not too bad) that you can take the derivative of any regular expression in a pretty straightforward way – like if you have (a+)|(b+), the derivative with repect to a is (a+). These derivatives turn out to combine in nice ways which is I guess why they are called derivatives.

When Kamal told me about taking the derivative of a string I FREAKED OUT for like 10 seconds and I was like “omg you can’t take the derivative of a string! WHERE EVEN IS THE LIMIT. OMG.” But now I have calmed down and it seems cool.

This library redgrep, I think, compiles regular expressions into LLVM bytecode by repeatedly taking the derivative of the regular expression to give you a DFA, when it then translates to LLVM. There’s a talk about it!. There are some pretty compelling examples of how it can take a complicated regular expression and translate it in to a pretty simple DFA.

The redgrep library is all C++ and is actually only a few thousands of lines of code, including tests. So I think it’s not actually that unapproachable to read the whole thing if you’re interested – the talk gives you a walk through of the code.

cool!

I wanted to write this up because I got this email, was like “this will take me a while to read”, and writing up my understanding has helped me understand it better! There is definitely a lot of interesting stuff to read in these Russ Cox articles. Time to go to sleep, though!